子供のイラストをスタンプに!!

最近、子供がLineのスタンプを自分で作れると知ってぜひやりたいと言い出したんですが、実際iPadをわたしてタッチペンで絵を描くのって難しいんですよね。鉛筆と勝手が違って。
泣きながら怒りながら、顔を赤くしてようやく1セット作りましたが本人はまだまだ不本意な様子。でももう懲りてやらないんだろうな~って思ってました。
手書きならたくさん書いてくれるんですよ。かわいい愛らしい絵をたくさん^^ 。
こんなのとか。

こんなのとか。

かわいいですよね~(笑)
これをそのままLineスタンプに出来たらな~と思ってました。
で、やっちゃいました!

なかなかイイ具合にできるのでは!?
そうはいっても結構コレ難しいんでしょ?と思われますよね?
ハイ、難しい、というか、めんどくさいです。
なのでこのページでは手書きイラストをLineスタンプにする手順を1ステップずつまとめておきました!
これで誰でもイラストをスタンプにできますよ!
折角書いてくれたかわいいイラスト。
そのままでしたら一定期間大事にとっておいた後、捨てるかしまったままにしておくか。。。
そうであればいっそのことスタンプにしちゃいましょう!
これで一生手元においておけるし、お友達に送ったりしても楽しいし!
なによりお子様も大喜びですよ(>▽<)!
このページを見ながら1ステップずつ一緒に進めてください!
きっとステキなスタンプができます!!
このページが参考になった!良かった!と思われた方は、ご寄付のつもりでこちらのたけのこボタンよりスタンプをご購入いただけますと嬉しいです!!

↑ Lovely illustration stampはこちら
では始めましょう!!
1.イラストを描く!
まずはイラストを描いてもらってください。
もちろん紙に描くんですよ!
すでに描いてあるものを集めてきてももちろんOK!
罫線付きのノートや広告の裏に描いたものでも多分大丈夫ですが、無地の紙に書いてあるもののほうがキレイにできます。
これをまず8個集めます。
イラストをスタンプにして販売するには8個、16個、24個、32個、40個のいずれかを1セットにする必要があります。
まずは8個を目指しましょう。
2.スマホで写真を撮ってパソコンに送る!
次にその写真をパソコンに取り込みます。
スキャナーを持っている人はスキャナーを使ってもOKですが、なかなか持ってませんよね。
絵をスマホで撮って、パソコンに転送したものでも案外うまく行きます(私はこの方法です)。
パソコンへの送信方法はUSBケーブルで直接パソコンにつなげるのが一番簡単かと思いますが、もしうまく行かないのであればメールで自分のメアドに送って、パソコンで開くという方法も簡単でオススメです。
3.編集ソフトをインストールする!
続いてパソコンでイラストを編集するためのソフトをインストールします。
ここではMediBang Paint for Proというソフトを使います。
フリーソフトです!ダウンロードはこちらのページの右上、”無料ダウンロード”ボタンからダウンロードしてください。
MediBang Paint for Pro
Windows (64bit), Windows (32bit), Macのうち、自分のパソコンに合わせてダウンロードします。
ダウンロードしたらダブルクリックしてインストール開始。
Microsoft Visual C++ 再頒布可能パッケージのインストールが必要です。というメッセージが出る事がありますが、もしこれが出たらそのまま再頒布パッケージと共にインストールを行ってください。
(もし再頒布インストールに失敗するようでしたら、一度インストールを中止してから、今度は再頒布パッケージをインストールしないにしてみてください。MediBangが立ち上がればOKです。)
うまくMediBang Paint Proはインストールできましたでしょうか?
有名なソフトですので、情報はたくさんGoogleで見つかります。
もしうまく行かなかったら、”MediBang Paint インストール”などでググってみてください。
4.初期設定して画像を読み込む
ではここからいよいよ本番!頑張りましょう!
まずソフトを立ち上げます。
コマーシャルが出てくるので、OKボタンを押して閉じます。
次にメディバンクラウド サービスという小窓が出てくるので、これも右上の×ボタンをおして閉じます。
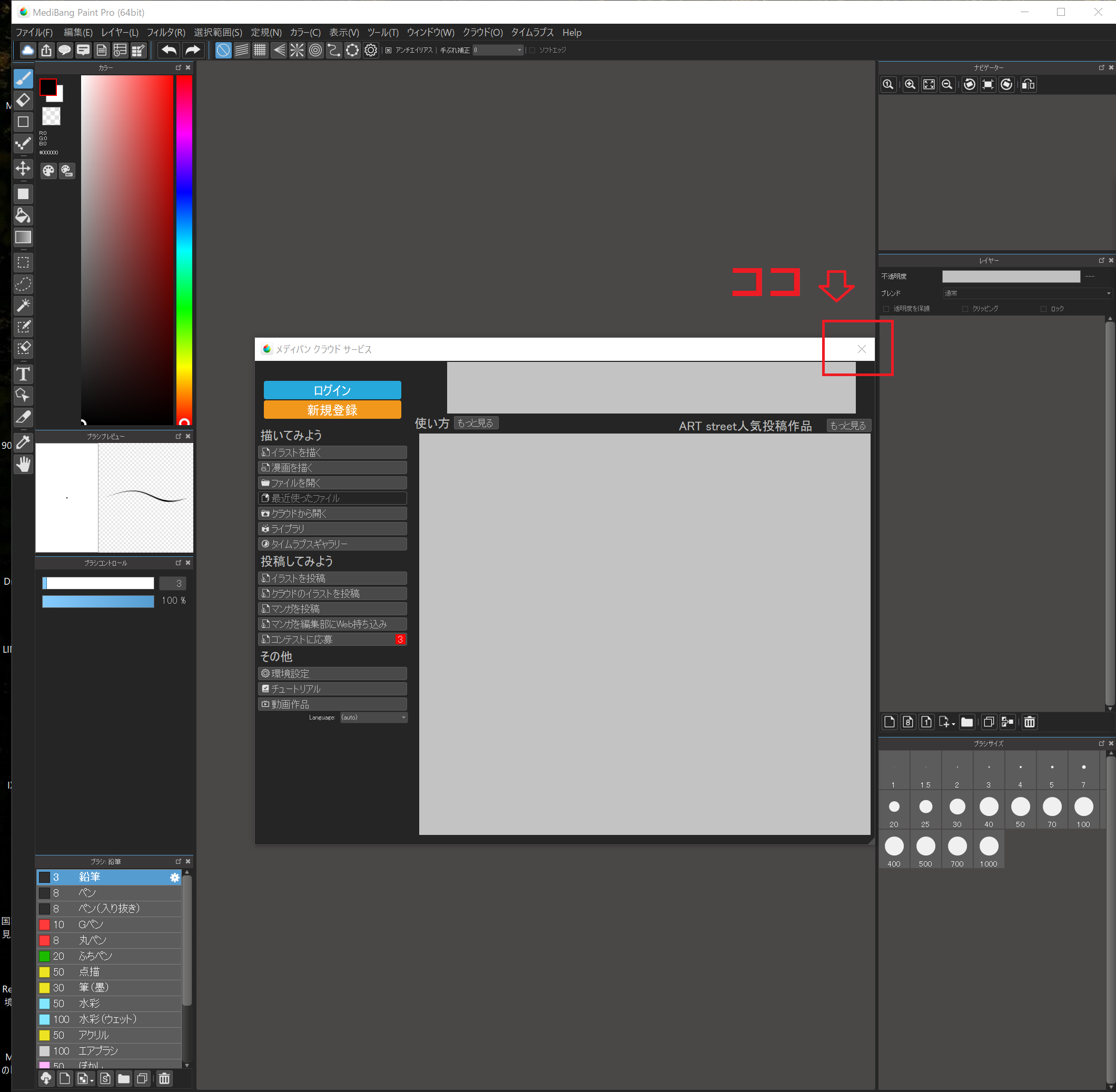
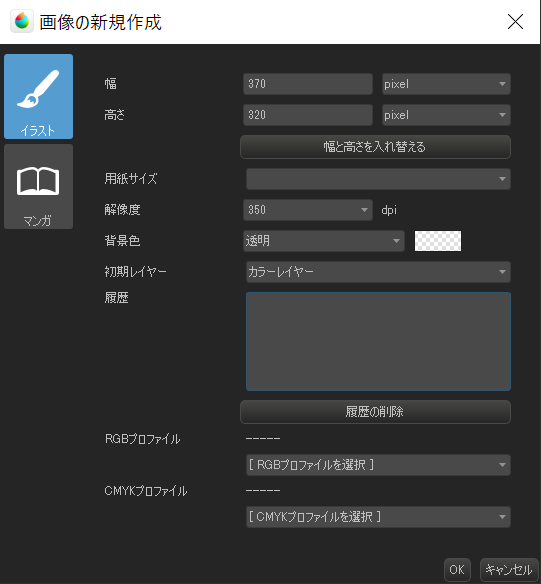
左上の”ファイル”から”新規作成”。
幅を370px, 縦を320pxにします。
これはLineスタンプのガイドラインからの要求なので、変更できません。
その他は変更せずにOKを押します。
キャンパスができました。
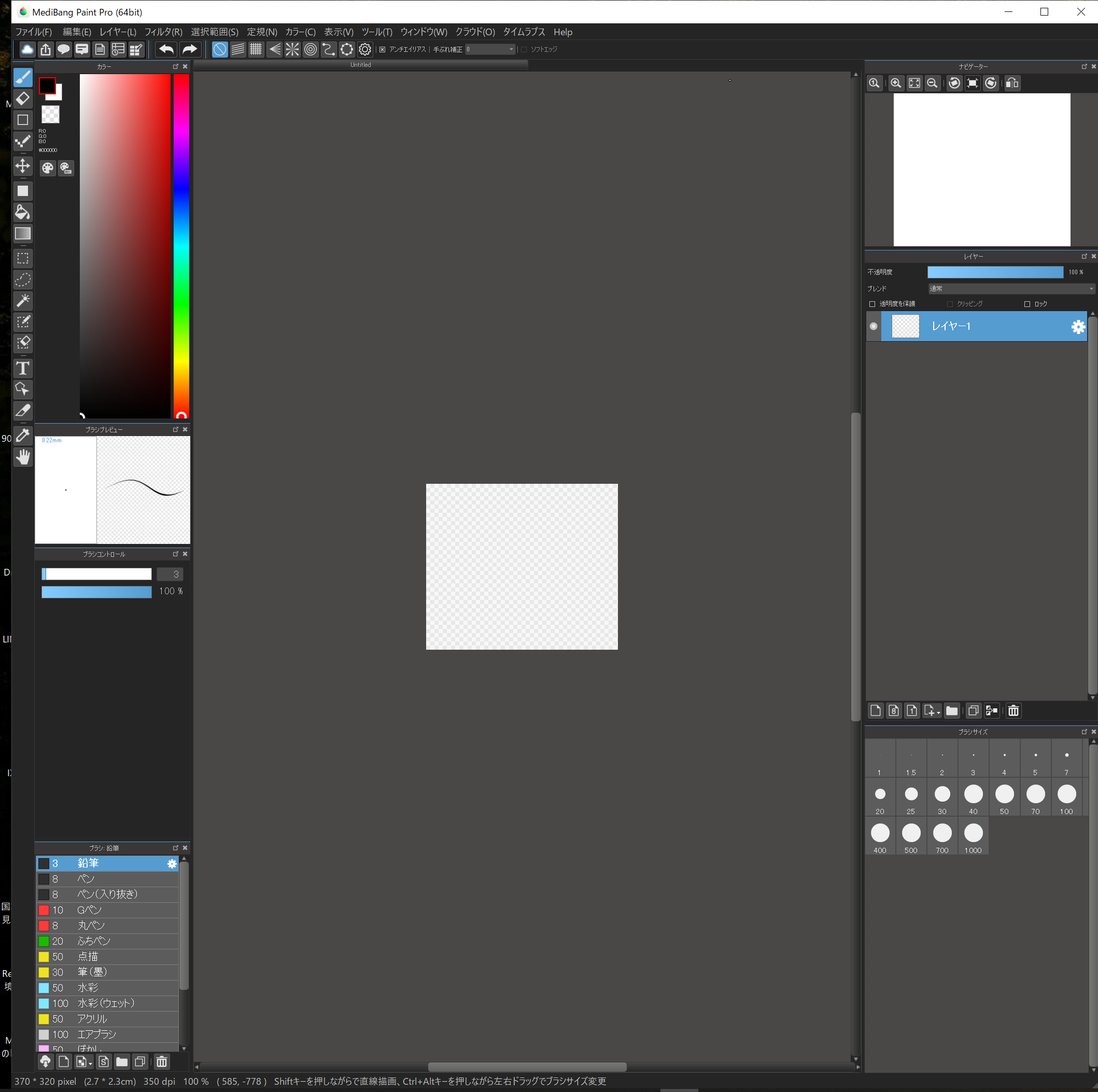
このキャンパスにスタンプの絵を作っていきます。
ここでいくつかマウス操作の確認。
拡大縮小→マウスのホイール
キャンパスの移動→シフトキーを押しながら左クリックのドラッグ
ブラシサイズの変更→Ctrl+Altを押しながら左ドラッグのまま左右に動かす
あたりを覚えておくと快適に作業ができます。
さあどんどん行きますよ。
左上の”ファイル”→”開く”
で、手書きのイラストをひとつ開いてください。
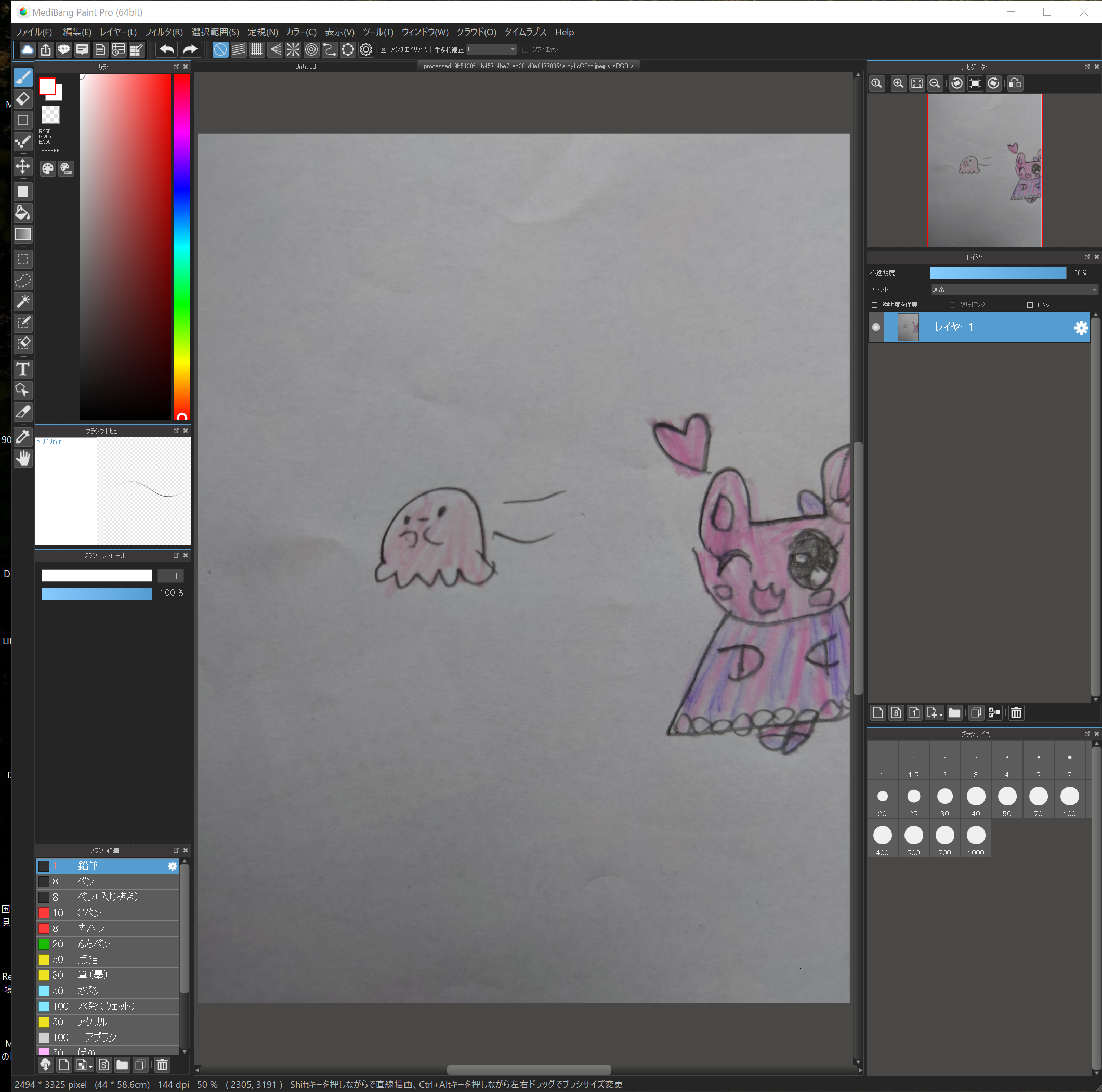
ここではこのタコさん?を使って説明しますね。
スタンプにしたいイラストの範囲を選択します。
左のツールから”選択ツール”を選択し、左ドラッグで範囲を指定してください。
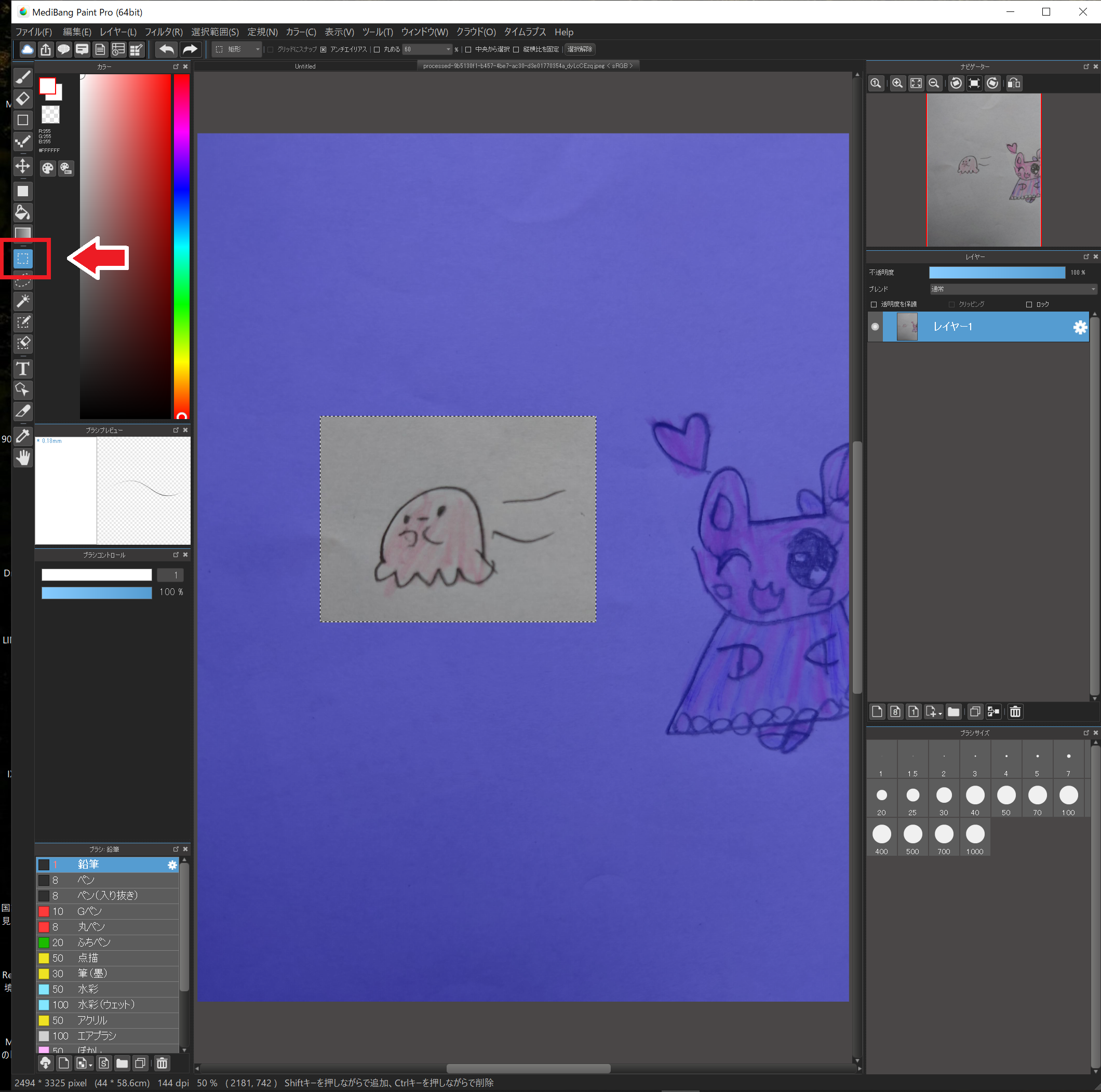
そして”編集”→”コピー”し、キャンパス上のタブから先ほど作った新しいキャンパスを選択します。
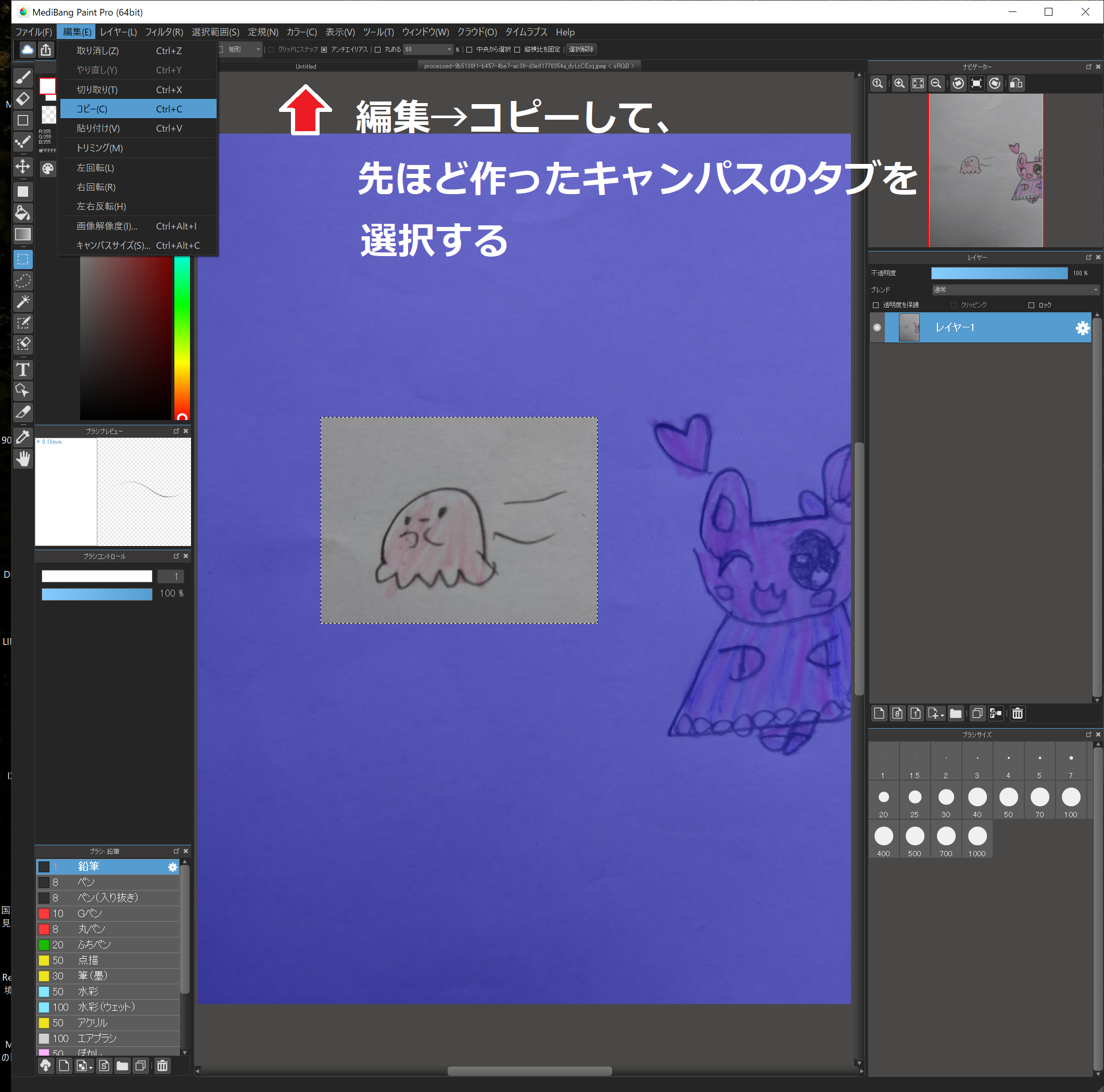
新しいキャンパスに張り付けます。
そのままではサイズが異なり、はみ出してしまうので縮小して、位置を合わせます。
“選択範囲”→”変形”で拡大・縮小・移動に加えて回転もできるようになります。
後で文字も入れるので、そのことも考慮しつつ、イイ感じの場所に配置してください。
これでOKと思ったらEnterを押して確定です。
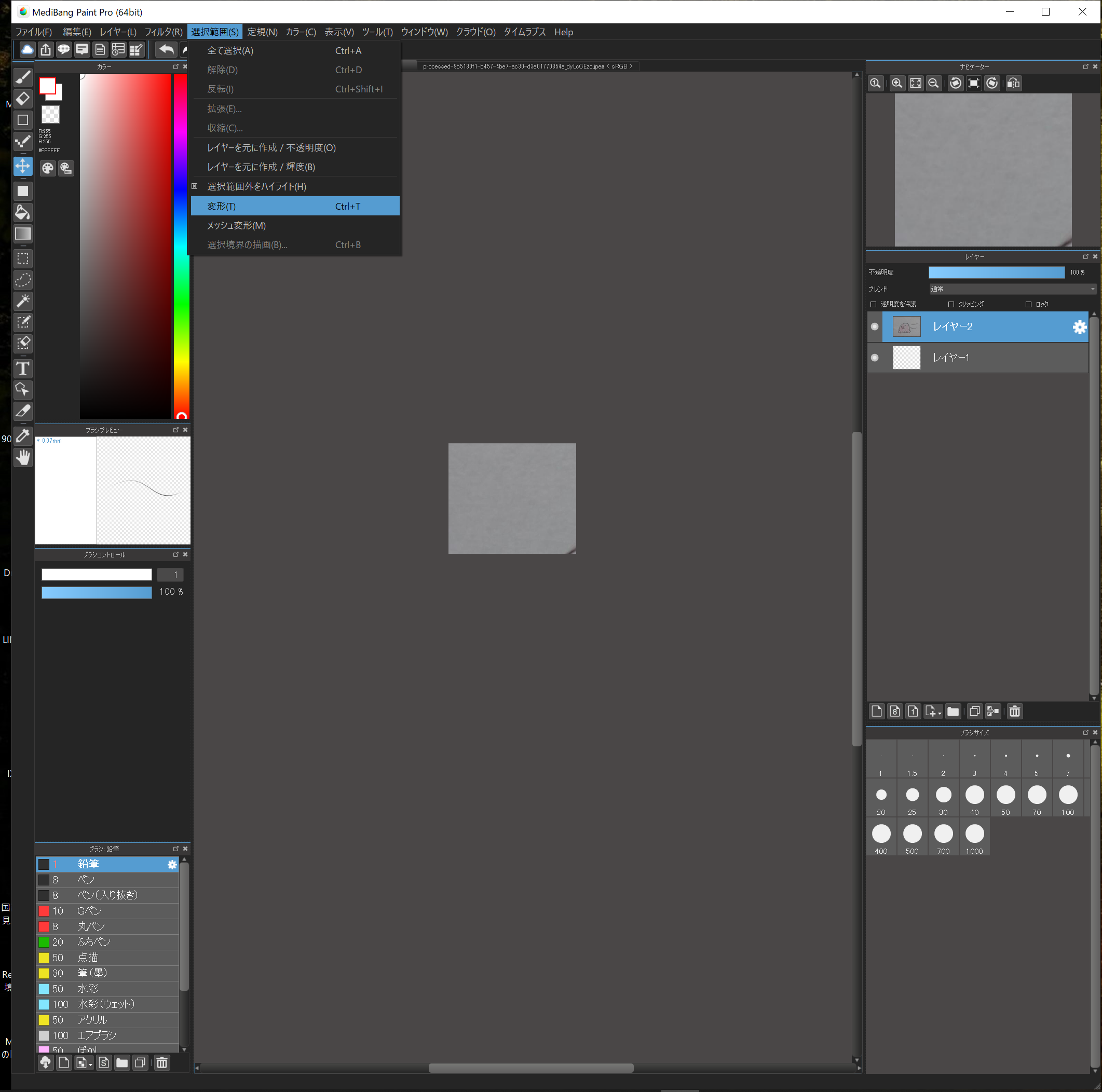
チェッカー模様になっているところは透明を表しています。
これで画像の取り込みは完了!
5.輪郭を抽出する
この元画像を加工していきます。念のためレイヤーを複製して、いつでもやり直しできるようにしておきましょう。
画像が表示されているレイヤーが選択されている状態(色が反転)で、”レイヤーの複製”で複製できます。
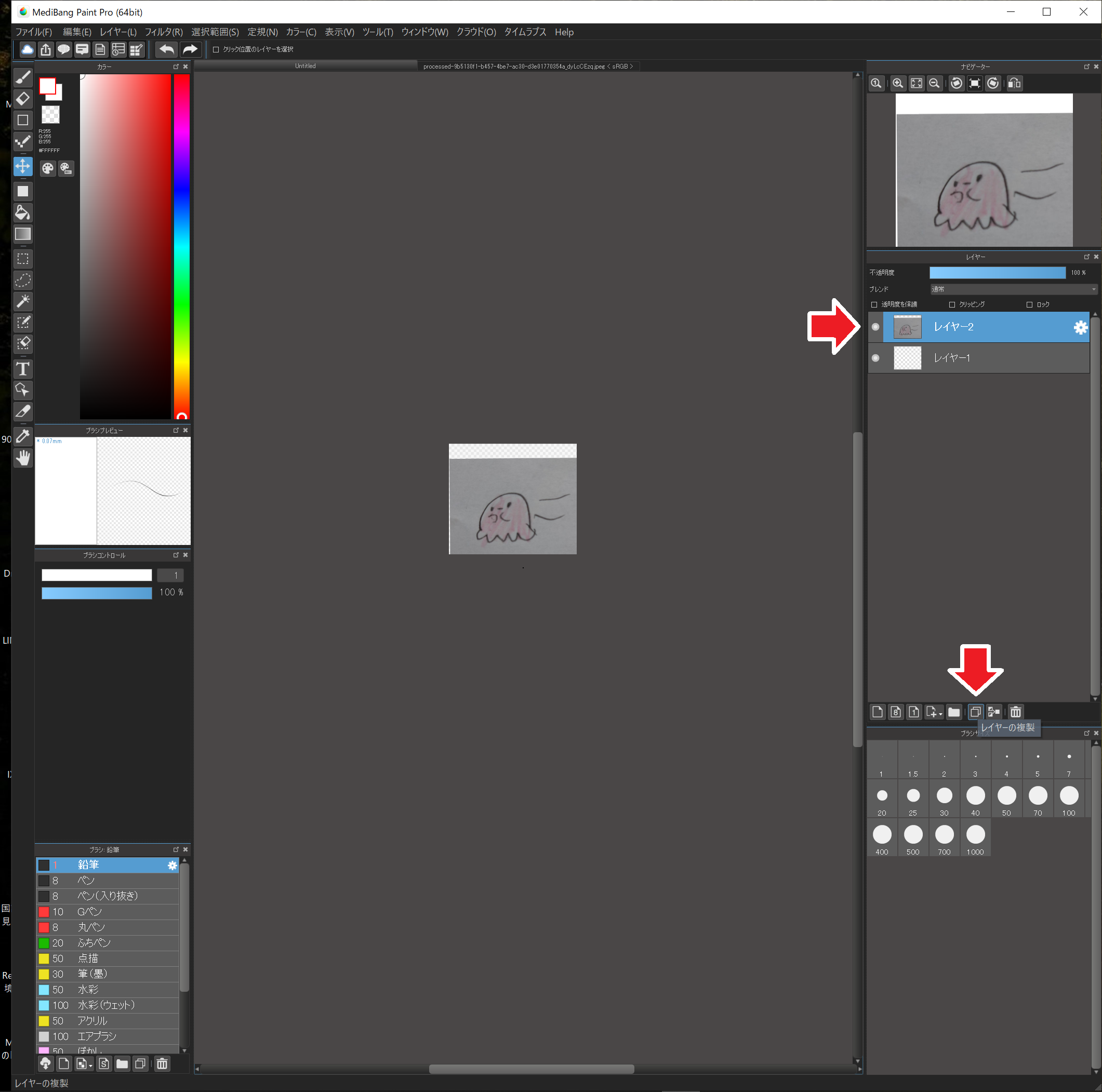
ここでちょっとレイヤーの解説。
レイヤーとはアニメのセルのようなもので、いくつかのレイヤーを重ねて1枚の画像を作る方法です。
上側のレイヤーと重なる下側のレイヤーは、上側のレイヤーの透明色に指定されている領域のみが最終的に表示されるようになります。
この機能を使うと、例えば背景、キャラ、文字など、いくつかの要素を別々のレイヤーで作っておいて、後で組み合わせるなどができるようになります。
レイヤーの左側の小さな丸ボタンは表示のオン・オフ機能で、この丸ボタンが表示されているレイヤーのみ、画面に表示されます。試しに付けたり外したりしてみてください。
手書きのイラストはどうしても輪郭がぼやけてしまうので、まずは輪郭の抽出から行います。
先ほどコピーした一番上のレイヤーを選択し、”レイヤー”→”変換”→”8ビットレイヤーに変換”します。
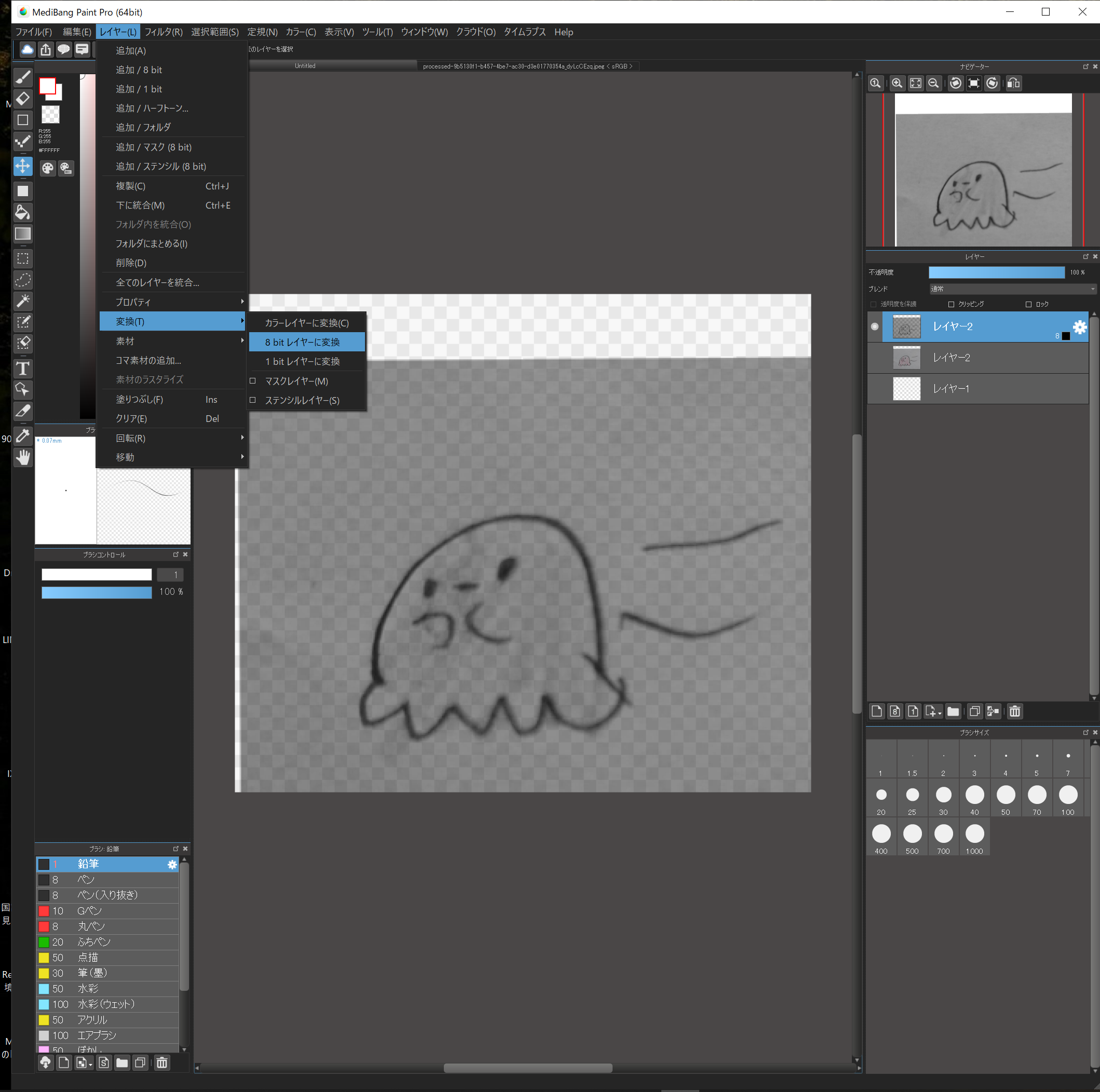
8bitレイヤーの下に白いレイヤーを作って見やすくします。
“レイヤーの追加”で無色のレイヤーを追加。
無色のレイヤー以外を非表示。
“バケツツール”を選択、左の色を白にし、無色のレイヤーを白く塗ります。
無色のレイヤーを8bitのレイヤーの下に移動します。
8bitのレイヤーを表示します。
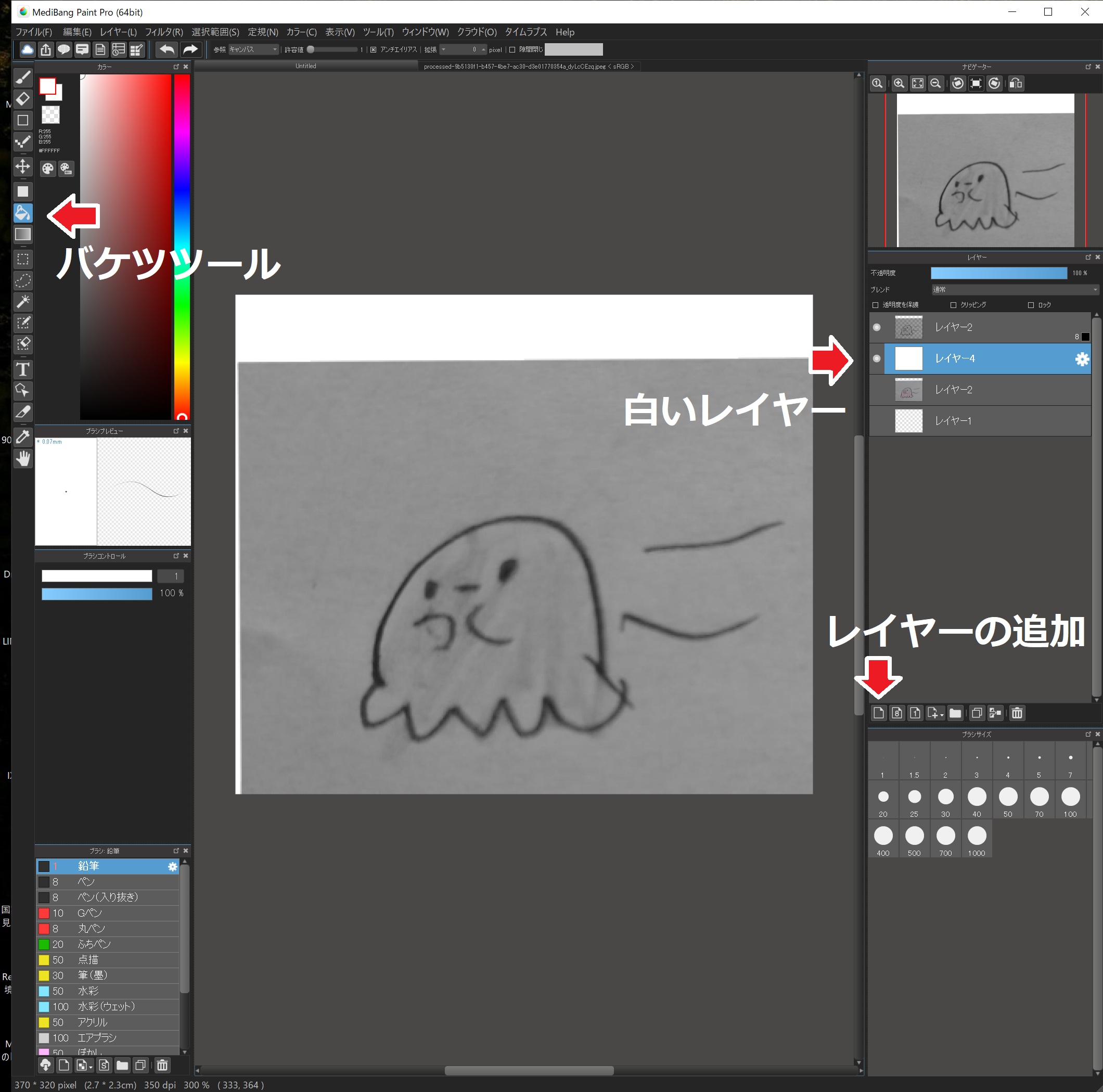
6.輪郭を抽出する2
“フィルタ”→”レベル補正”で入力の欄の矢印を調整します。
ここで背景、イラストの色を白飛びさせ、輪郭だけが残るように調整してください。
輪郭が消えかかっても大丈夫。
背景と色をしっかりと飛ばすのがポイントです。
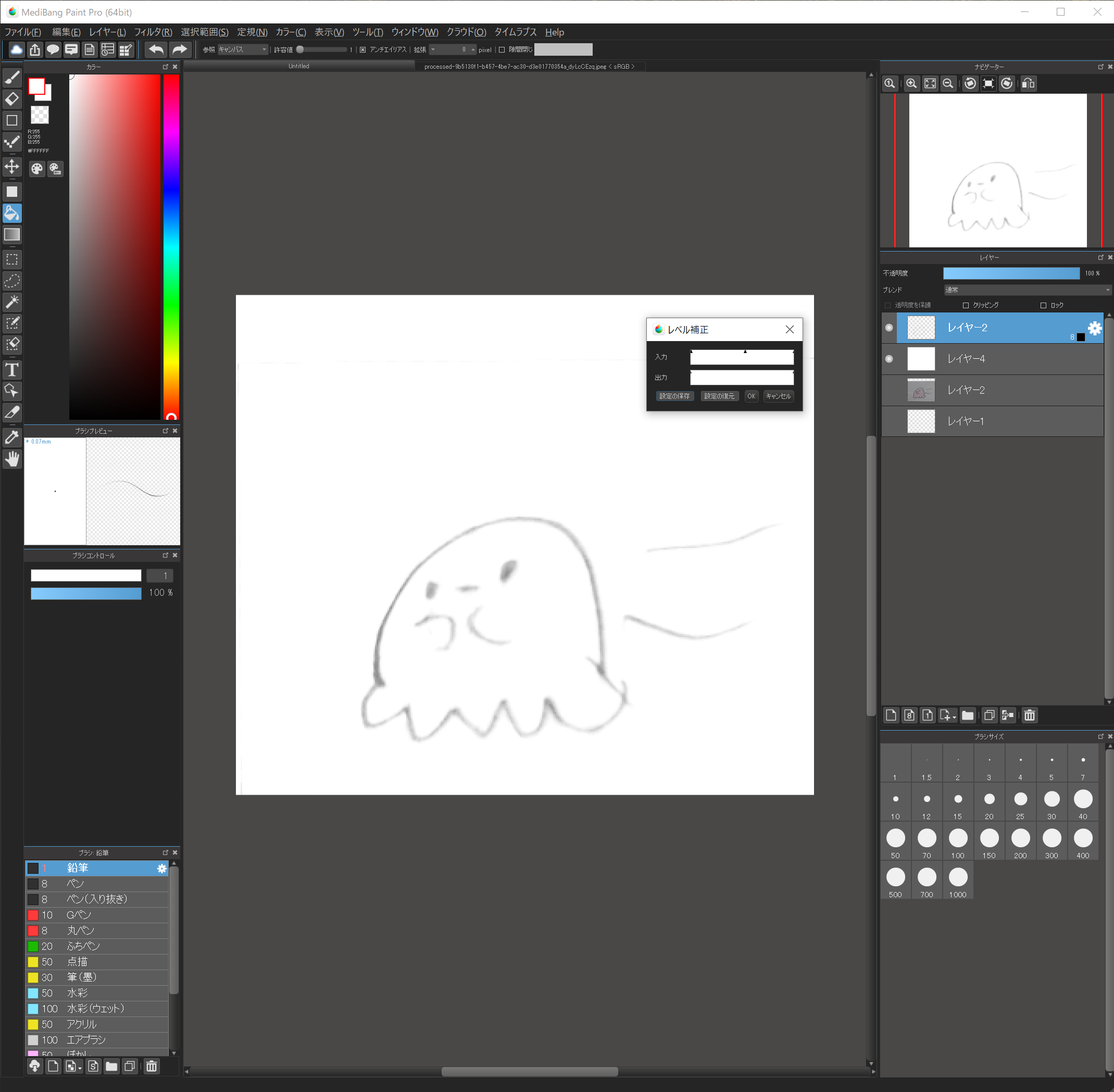
ちょっと難しいですけど、何度もやってみるとそのうちコツがつかめると思います。
この後、”選択範囲”→”レイヤーを基に作成/輝度”を実行して、輪郭が選択されればOKです!
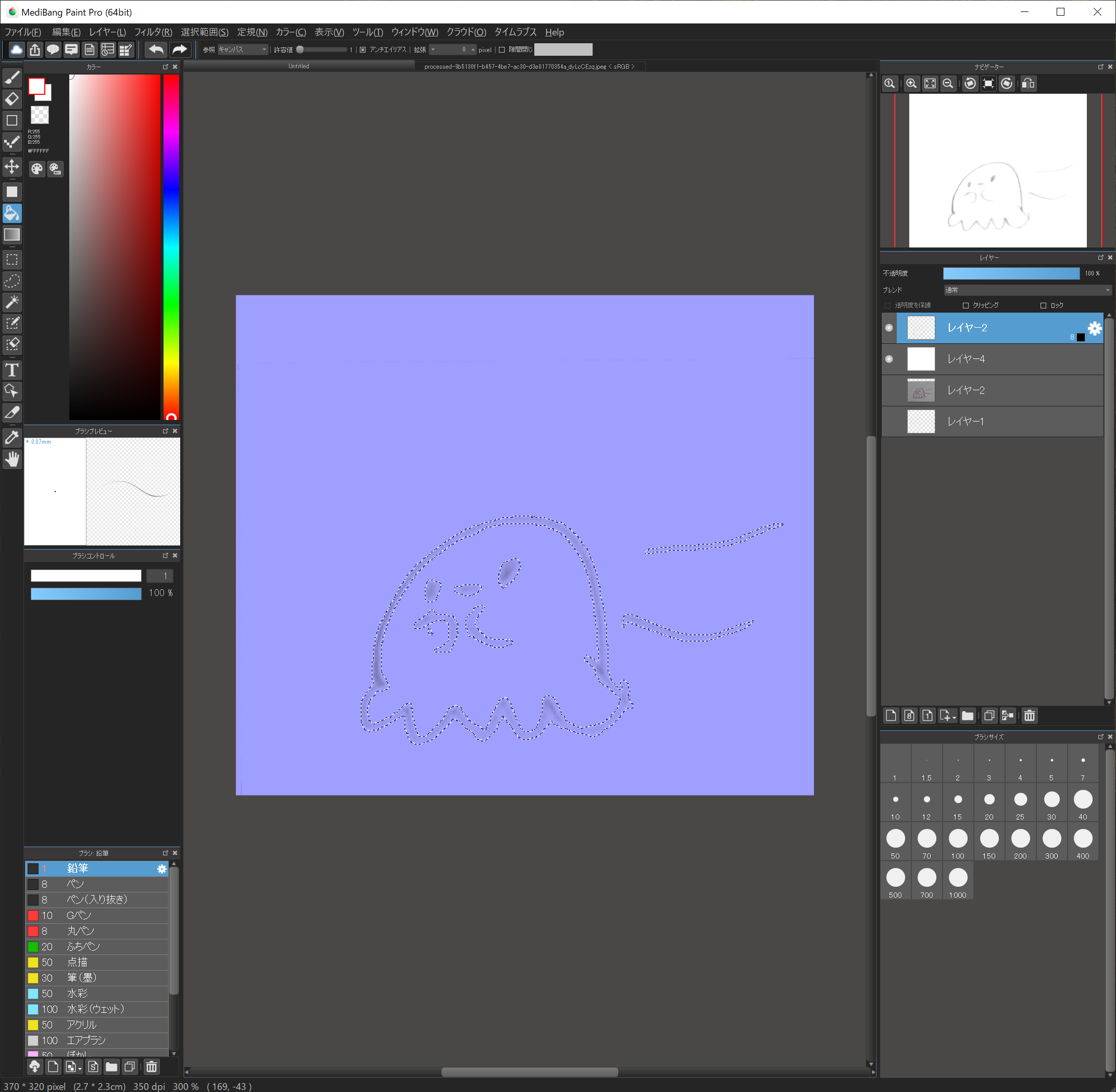
この時、わずかに余計な部分が選択される場合もありますが、多少であれば問題ありません。
元絵の色が濃い時などでうまく輪郭が抽出されない場合は、この方法ではなく、”投げ縄ツール”や”自動選択ツール”などを使って輪郭を抽出してみてください。
7.輪郭を抽出する3
輪郭を黒で塗ります。
輪郭が選択されたまま、ブラシで黒く塗ります。
背景が透明なレイヤーに塗ってください。
輪郭が選択されているので、選択範囲外は塗ることができません。
なので、ブラシで雑に塗っても輪郭だけがキレイに塗れる事になります。
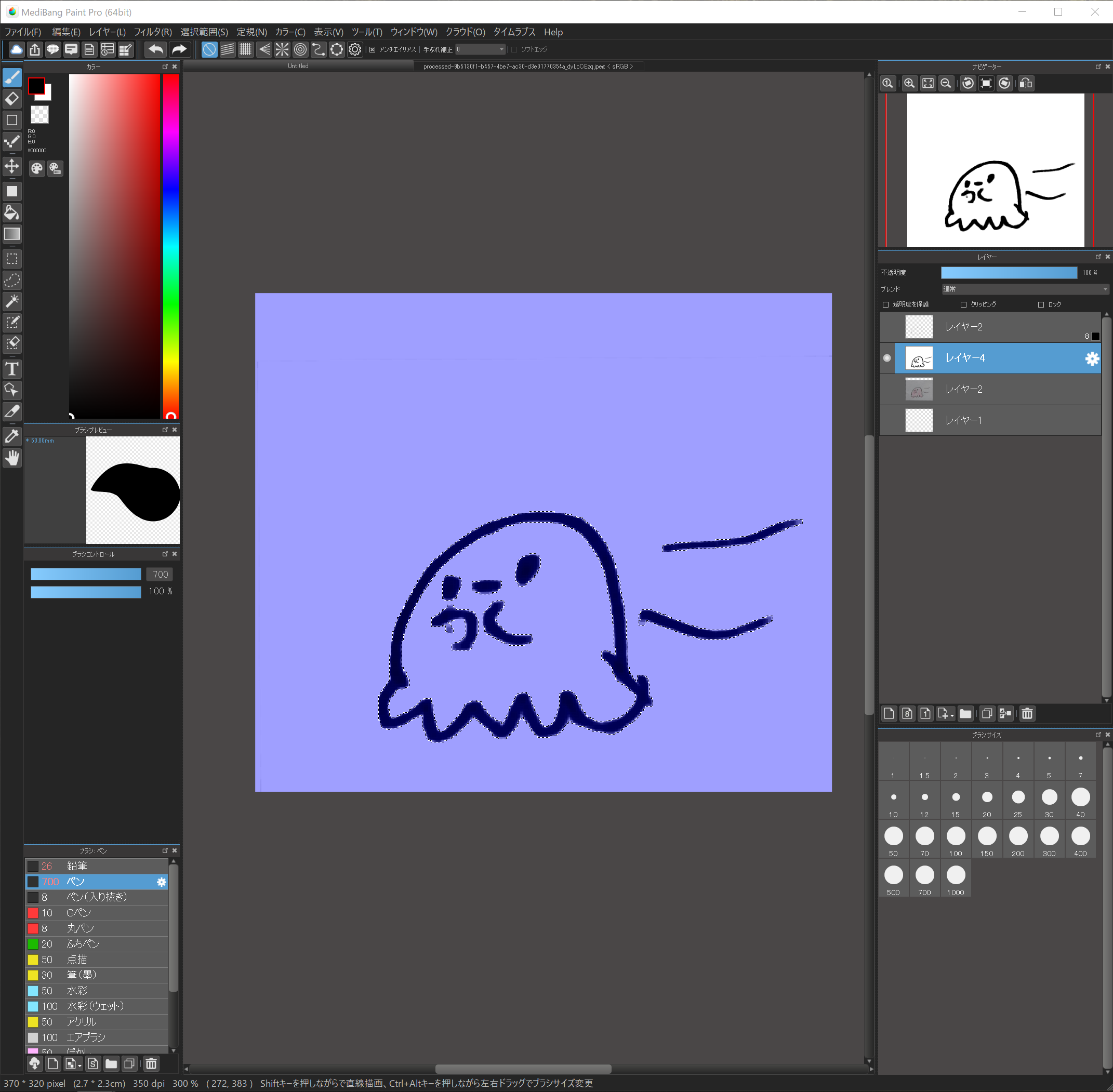
できましたでしょうか?
ちょっとしたはみだしなどは選択範囲を解除してから、ここで修正していきます。
輪郭だけが黒く塗られ、他は透明色になっている状態にしてください。
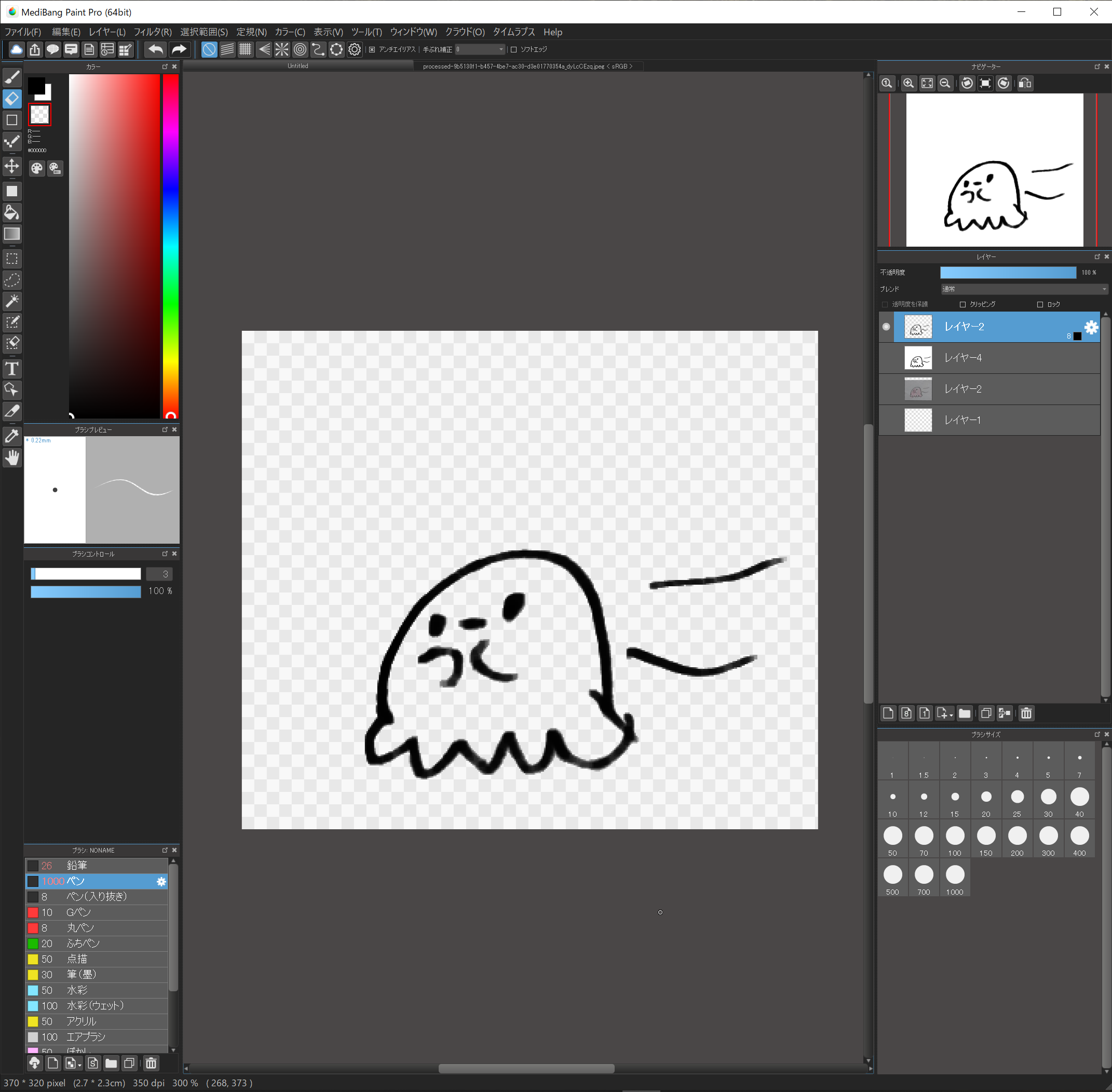
8.元絵の背景を消す
元絵の背景を消します。
輪郭を抽出したレイヤーを選択し、自動選択ツールを選択、背景を選択します。
元絵のレイヤーを選択し、バケツツールで背景を透明色にしていきます。
この時、許容値の値を10程度にしておくと、背景に色むらがあっても上手に透明色にしてくれます。
ちょっと残った場合もブラシで透明色を塗ればOKです!
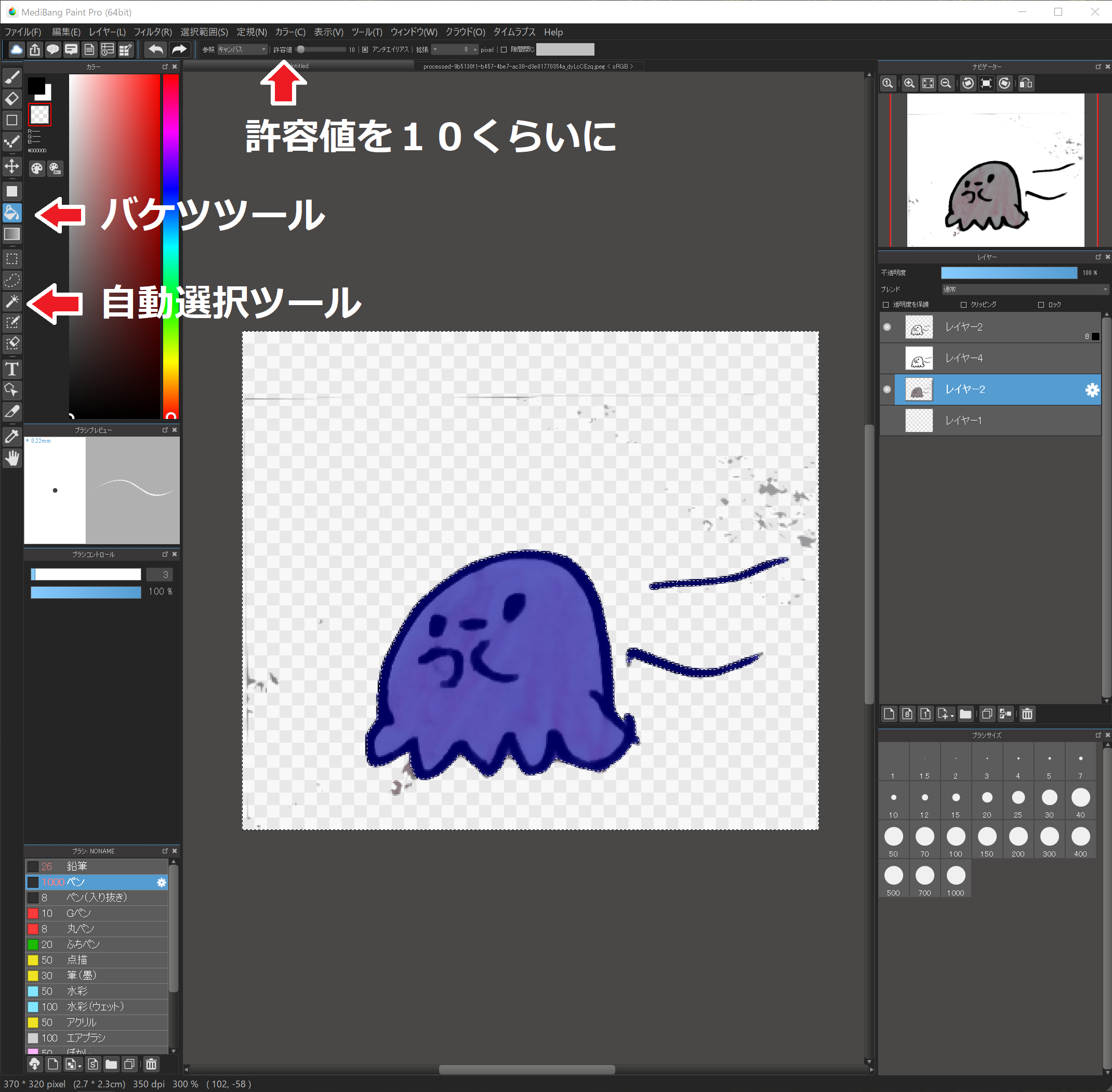
9.色を付ける
色を付けていきます。
もし元絵に色がついていない場合は、ここでブラシツールなどで直接色をつけちゃいましょう!
元絵に色がついている場合はせっかくなのでそれを活かしたいと思います。
“フィルタ”から”レベル補正”、”色相”、”トーンカーブ”あたりを調整し、元絵の色を出していきます。
子供の絵ですから、鮮やかな色の方がいいですね。
色々試して、キレイな色を探してみてください!
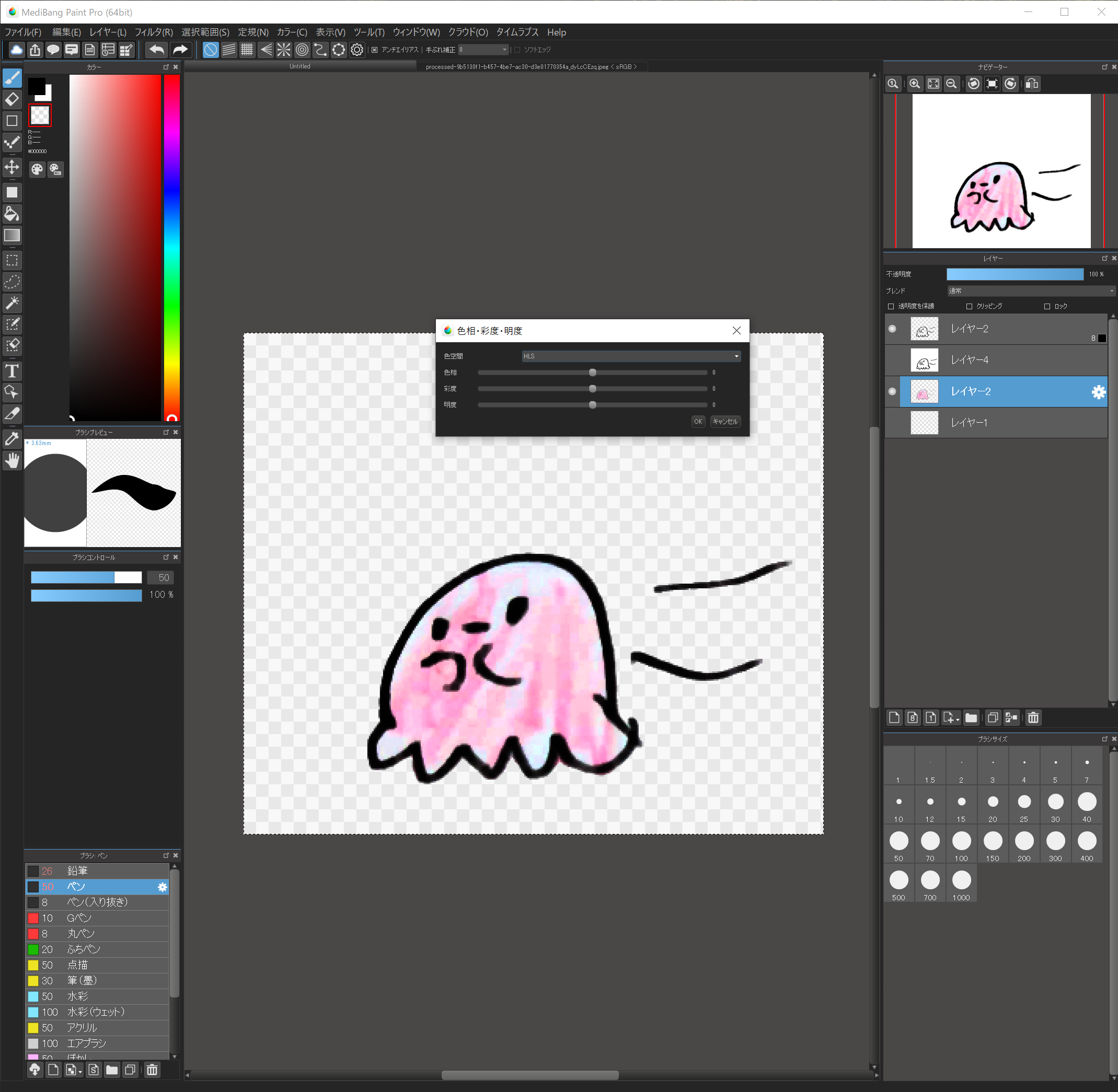
10.文字を入れる
ついてきてますか~!
かわいい絵をスタンプにするためです!
頑張ってください~!
文字を入れます。
“テキスト編集”を押し、文字を入れたい場所をクリックします。これは後で移動できます。
初めての場合は”クラウドテキストを使用する”にチェックが入っていますので、これを外します。
フォント名はHG創英角ポップ体、文字サイズは12pt、文字色は黒、ふち幅は3、ふち色は白を選択します。
その下に文字を入力すると文字が入ります。
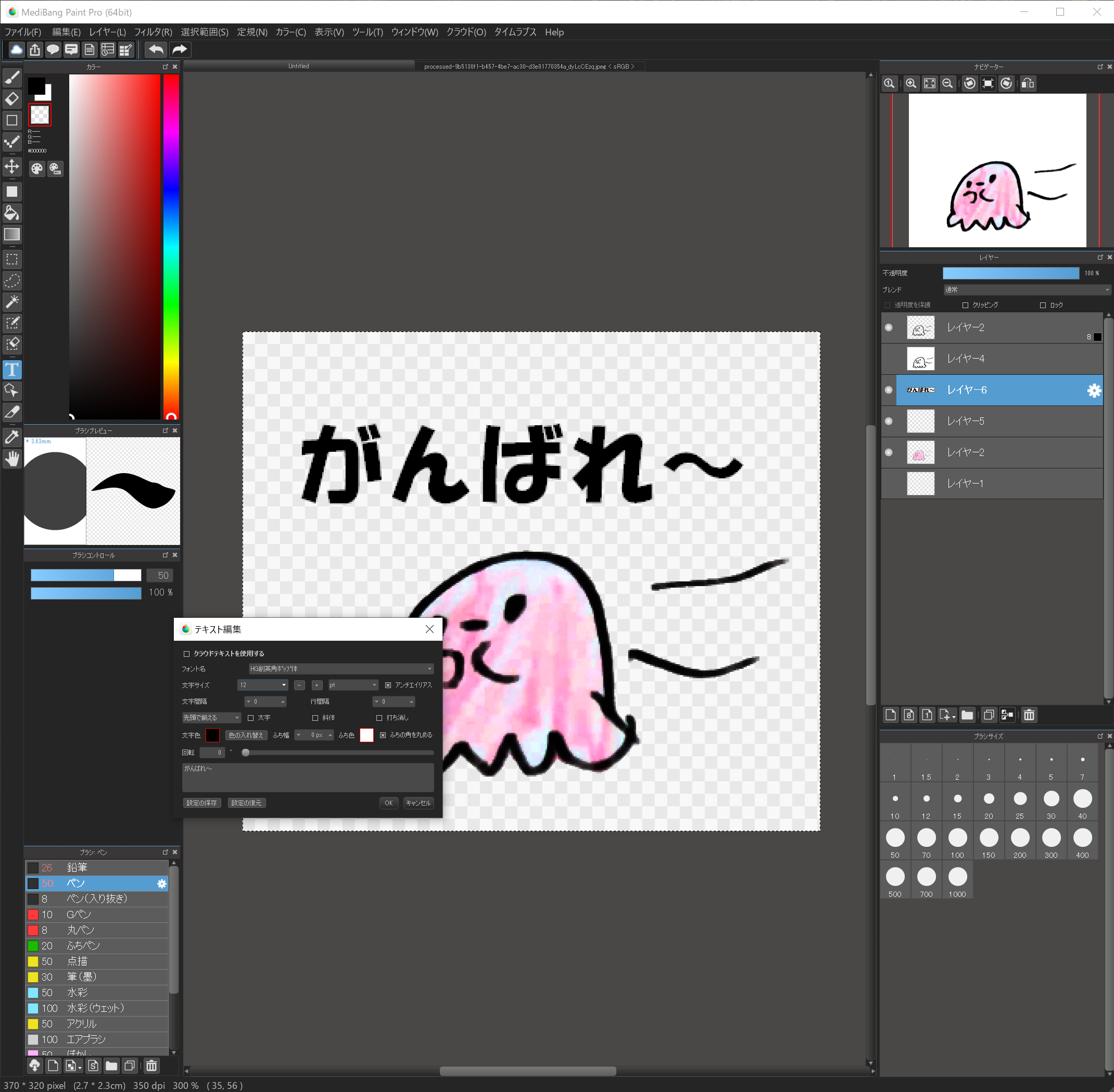
もちろんフォントやサイズ、色は変更して大丈夫なワケですが、ふち幅は必ず設定してください。
スマホの背景は人の設定によって変わりまして、黒い背景にしている人に使ってもらった場合、ふち幅が設定していなかったら文字が消えてしまいます。
11.イラストにしろいふちを付ける
文字には白いふちを付けましたが、イラストにもつけておかないと、人によっては背景でイラストが隠れてしまいます。白いふちを付けましょう。
色をつけたレイヤーを選択、自動選択ツールで背景を選択、
選択範囲→反転
選択範囲→拡張→3pixel
レイヤーを複製して、複製したレイヤーを選択
下側にあるレイヤーを選択して、選択範囲を白く塗りつぶします。
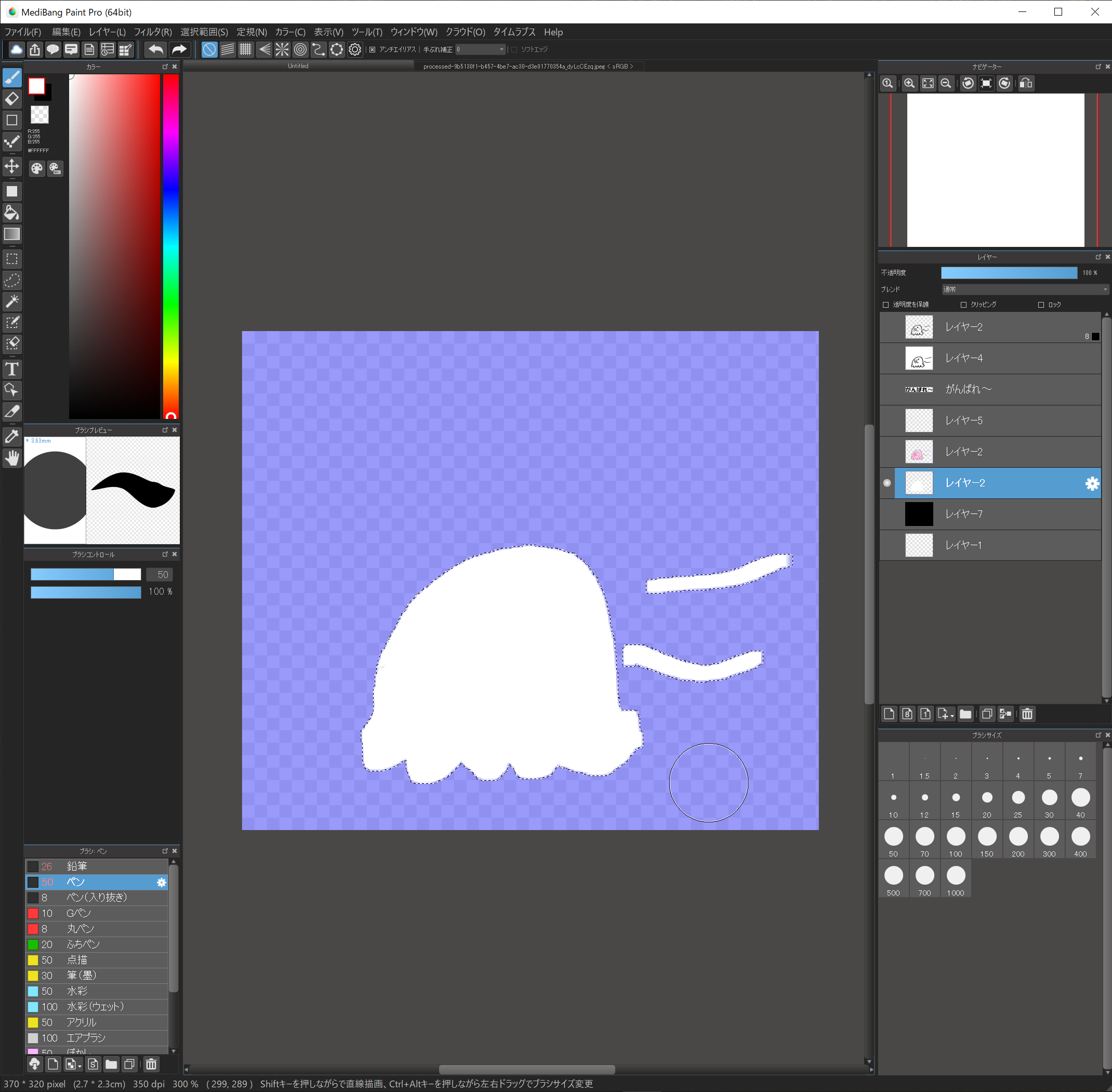
12.確認!
非表示にしていたレイヤーを表示して、全体を確認してください。
うまくできましたでしょうか?
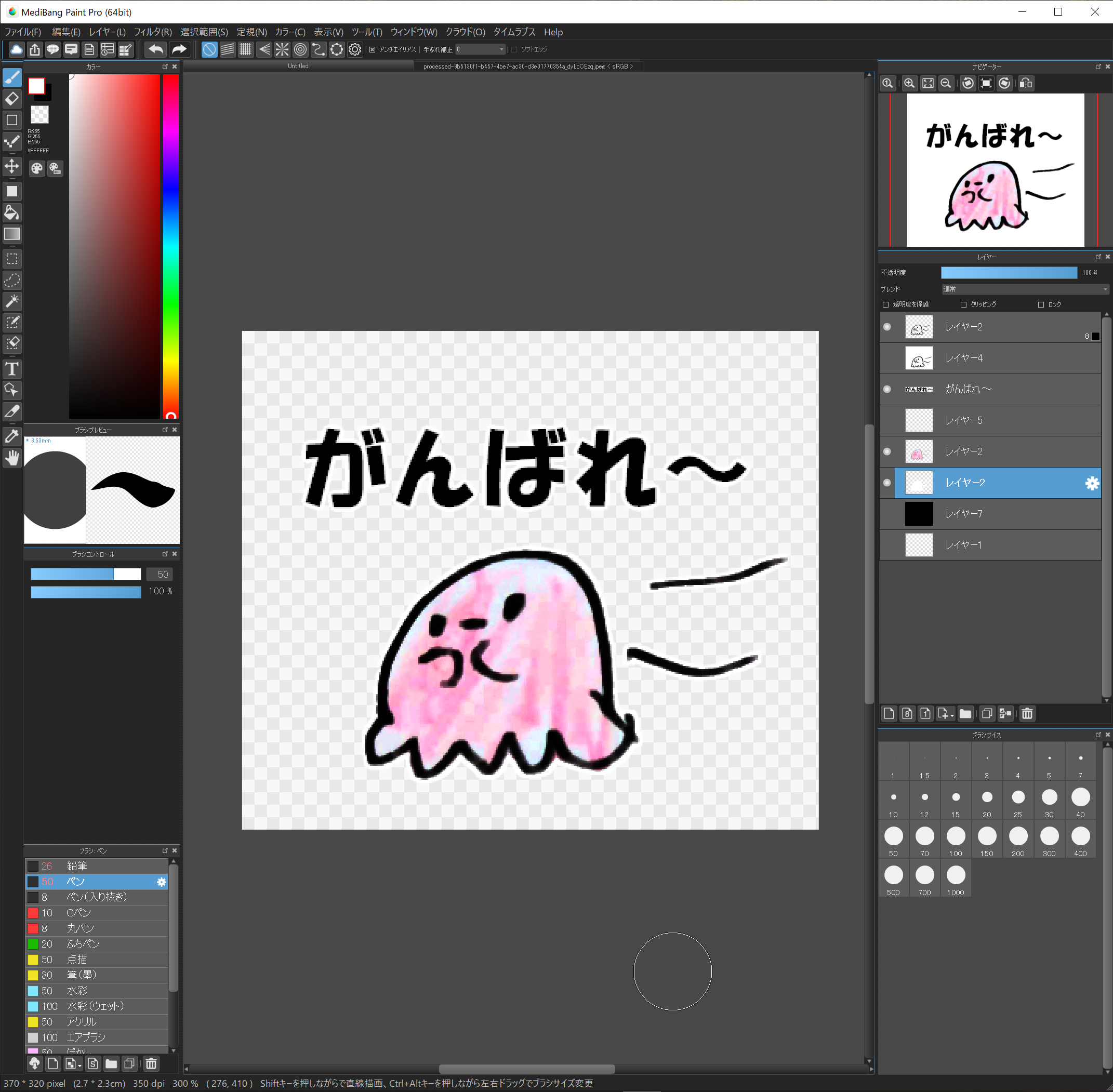
13.pngで保存
最後にpng形式で保存します。
“ファイル”→”名前を付けて保存”
ファイルの種類をpngにし、適当な名前をつけます。
“この形式はレイヤーが保存されませんが、よろしいですか?”は”はい”。
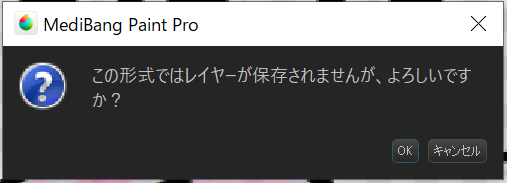
“保存設定”は”透過PNG”
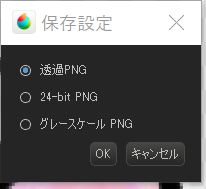
これで1つできました!お疲れ様でした!!
14.素材を揃える
これを繰り返し、全部で8つ作る必要があります。
初めは少し大変なのですが、慣れればどんどん早くできるようになります。
最後に、実はこれ以外にもメイン画像とタブ画像を作る必要があります。
メイン画像は横240px、縦240pxの画像。
タブ画像は横96px、縦74pxとなります。
ここまでのやり方と同じで、キャンパスサイズを変えて作ってください。
もちろん、今までの素材を使って、少し編集するだけでも良いと思います。
全部できたら用意する素材は揃いました!!!
15.Lineに登録する
スタンプにしたい画像を8個以上、メイン画像1個、タブ画像1個ができたら、あとは登録するだけです。
登録はLine Creators Marketで行います。
Line Creators Market
登録の仕方ですが、これは先人がたくさん分かりやすいページを作っていますので、ここでは省略したいと思います。Googleで”Line スタンプ 登録”で出てくるサイトを参考にしてください。
16.さいごに
簡単!子供の手書きイラストをLineスタンプにしよう!は以上になります。
いかがだったでしょうか?
一見難しく見えるかもしれませんが、やってみるとそうでもありませんし、すぐに慣れると思います。
このひと手間でかわいいイラストがラインスタンプとして使えるようになると思えば!
きっと楽しい宝物になりますよ!!
このページが良かった!参考になった!と思われた方は、ご寄付のつもりでこちらのたけのこボタンよりスタンプをご購入いただけますと嬉しいです!!

↑ Lovely illustration stampはこちら
それではステキなラインライフを!



























